Interval exchange transformations

Introduction

This file is a good entry point to learn how to use interval exchange transformations in surface-dynamics. Recall that an interval exchange transformation is a piecewise translation of an interval. It can be encoded by a pair \((\pi, \lambda)\) where \(\pi\) is a permutation and \(\lambda\) is a vector of positive real numbers. These are respectively called the combinatorial datum and the length datum of the interval exchange transformation.

Building an interval exchange transformation and simple manipulations

Here is an example of interval exchange transformation on 4 subintervals with rational lengths

from surface_dynamics import iet
perm = iet.Permutation('a b c d', 'd c b a')
length = [1/3, 2/7, 4/13, 5/19]
t = iet.IntervalExchangeTransformation(perm, length)
print(t)

Interval exchange transformation of [0, 6172/5187[ with permutation
a b c d
d c b a

It can be visualized with:

G = t.plot_function()
G.set_aspect_ratio(1)
G # random (matplotlib warning in conda)
t.plot_two_intervals()

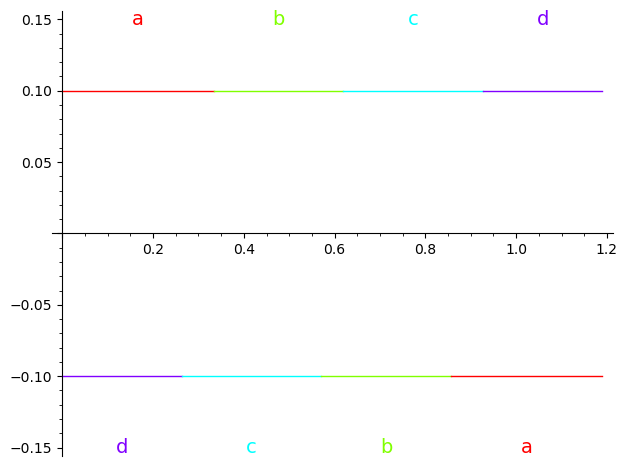
Given a point in the interval \([0, 6172/5187[\) it is possible to compute its image under the map \(t\)

x = 1/12
t(x)

19501/20748

To know which translation has been applied to the point \(x\) you can use

print(t.in_which_interval(x))
print(t.translations())
print(x + t.translations()[0] == t(x))

a
(1481/1729, 176/741, -142/399, -253/273)
True

Can you compute the first 20 elements of the orbit of \(x\), that is the sequence \((x, t(x), t^2(x), \ldots, t^{19}(x))\)?

Can you determine whether the orbit of :math:x is periodic, that is whether there exists \(n > 0\) such that \(t^n(x) = x\)?

To construct an interval exchange on other numbers than rationals you need to manipulate exact real numbers. The current sage version (9.2) only supports computation with algebraic numbers such as

x = polygen(QQ)
K.<sqrt2> = NumberField(x^2 - 2, embedding=AA(2).sqrt())
length2 = [1, sqrt2, sqrt2**2, sqrt2**3]
t2 = iet.IntervalExchangeTransformation(perm, length2)
print(t2)

Interval exchange transformation of [0, 3*sqrt2 + 3[ with permutation
a b c d
d c b a

Rauzy induction and self-similar iet

Rauzy induction is a map from the space of interval exchange transformations to itself. The image \(\mathcal{R}(t)\) of an iet \(t\) is an induced map.

t3 = t2.rauzy_move()
r = max(set(flatten(t2.singularities())) - set([0,3*sqrt2+3]))
G = t2.plot_two_intervals() + t3.plot_two_intervals(position=(0,-.8))
G += line2d([(r, -1.), (r, .2)], color='black', linestyle='dotted')
G.axes(False)
G

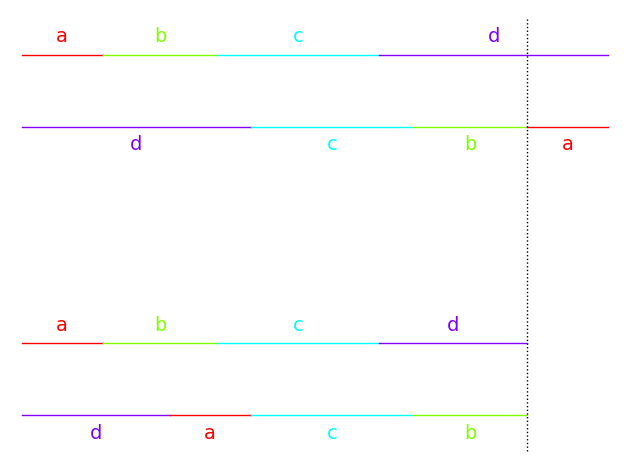
From a flip sequence given combinatorially you can build the associated self-similar interval exchange transformation

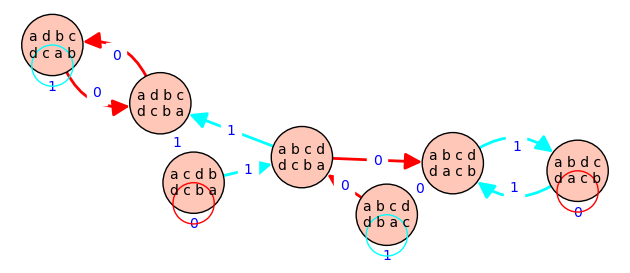
R = perm.rauzy_diagram()
G = R.graph()
P = G.plot(color_by_label=True, edge_labels=True, vertex_size=800)
P

seq = ['t', 'b', 't', 'b', 't', 't', 'b', 'b', 't', 'b']
f = iet.FlipSequence(perm, seq)
print(f.is_loop())
print(f.is_full())

True
True

dilatation, t4 = f.self_similar_iet()
print(dilatation, '~', dilatation.n())

3*a + 2 ~ 6.85410196624968

Above dilatation is the expansion of the self-similarity and t4 is the self-similar exchange transformation associated to the flip sequence f

t5 = t4.rauzy_move(iterations=len(seq))
G = t4.plot() + t5.plot(position=(0,-.5))
G.axes(False)
G

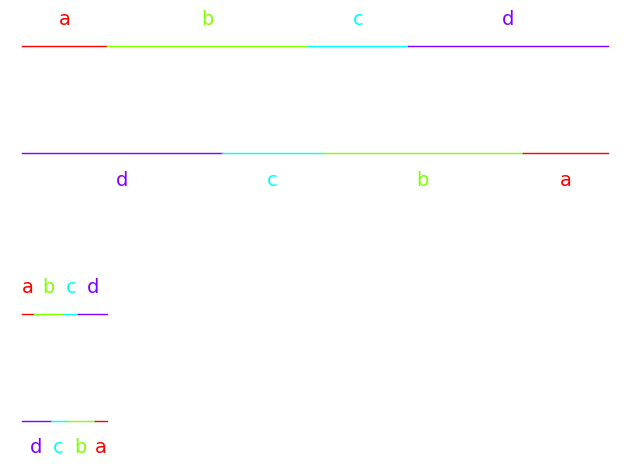
print(t4.lengths())
print(t5.lengths())
print(dilatation * t5.lengths() == t4.lengths())

(1, 6/5*a + 2/5, 3/5*a + 1/5, 6/5*a + 2/5)
(-3*a + 5, 6/5*a - 8/5, 3/5*a - 4/5, 6/5*a - 8/5)
True

The command below checks that t4 is indeed self induced

print(t4.normalize() == t5.normalize())

True

Suspension

sage-flatsurf is a Python library for translation surfaces (and more generally similarity surfaces). One can build Masur polygons via

height = [1, 0, 0, -1]
S = perm.masur_polygon(length2, height)
S
S.stratum()

H_2(2)

Could you construct a self-similar translation surface from the flip sequence f? (in other words a translation surface that admits a pseudo-Anosov preserving the horizontal and vertical foliations)

Using pyintervalxt

intervalxt is a C++ library with a Python interface that implements optimized routines to deal with interval exchange transformations. If intervalxt is part of your installation you can convert interval exchange transformations back and forth between surface-dynamics and pyintervalxt

from surface_dynamics.interval_exchanges.conversion import iet_to_pyintervalxt, iet_from_pyintervalxt
u2 = iet_to_pyintervalxt(t2)
print(u2)
v2 = iet_from_pyintervalxt(u2)
print(v2)

(Re-)building pre-compiled headers (options: -O2 -march=native); this may take a minute ...

warning: unknown warning option '-Wno-enum-constexpr-conversion' [-Wunknown-warning-option]

warning: unknown warning option '-Wno-enum-constexpr-conversion' [-Wunknown-warning-option]

/home/runner/work/surface-dynamics/surface-dynamics/.pixi/envs/dev/lib/python3.12/site-packages/cppyy/__init__.py:341: DeprecationWarning: pkg_resources is deprecated as an API. See https://setuptools.pypa.io/en/latest/pkg_resources.html
  import pkg_resources as pr

/tmp/ipykernel_4773/1501804959.py:2: DeprecationWarning: the function is_NumberField is deprecated; use isinstance(x, sage.rings.number_field.number_field_base.NumberField) instead
See https://github.com/sagemath/sage/issues/35283 for details.
  u2 = iet_to_pyintervalxt(t2)

[a: 1] [b: (sqrt2 ~ 1.4142136)] [c: 2] [d: (2*sqrt2 ~ 2.8284271)] / [d] [c] [b] [a]
Interval exchange transformation of [0, 3*sqrt2 + 3[ with permutation
a b c d
d c b a

One feature of intervalxt is that it can certify that an iet has no periodic trajectory

u2.boshernitzanNoPeriodicTrajectory()

True

Other features

This short tour did not exhaust all the possibilities of surface-dynamics, in particular

• iet statistics (in surface_dynamics.interval_exchanges.integer_iet)

• linear families of iet (in surface_dynamics.interval_exchanges.iet_family)

• coverings and Lyapunov exponents of the Kontsevich-Zorich cocycle

These topics might be included in later versions of this document.

Missing features

• generalizations (linear involution associated to generalized permutations, interval exchange transformations with flips, affine iet, system of isometries)

• Veech zippered rectangle construction

• constructing the self-similar surface (aka pseudo-Anosov) associated to a flip sequence

If you are interested in developing any of these or have any request, get in touch with us at https://github.com/flatsurf/surface-dynamics