tangent_bundle

class flatsurf.geometry.tangent_bundle.SimilaritySurfaceTangentBundle(similarity_surface, ring=None)[source]

Construct the tangent bundle of a given similarity surface.

Needs work: We should check for coercion from the base_ring of the surface

base_ring()[source]
clockwise_edge(polygon_label, edge_index)[source]

Return the vector leaving a vertex of the polygon which under straight-line flow travels clockwise around the boundary of the polygon along the edge with the provided index. The length of the vector matches the length of the indexed edge. Note that the point will be based in the polygon opposite the provided edge.

EXAMPLES:

sage: from flatsurf.geometry.similarity_surface_generators import SimilaritySurfaceGenerators
sage: s = SimilaritySurfaceGenerators.example()
sage: from flatsurf.geometry.tangent_bundle import SimilaritySurfaceTangentBundle
sage: tb = SimilaritySurfaceTangentBundle(s)
sage: s.polygon(0)
Polygon(vertices=[(0, 0), (2, -2), (2, 0)])
sage: s.polygon(1)
Polygon(vertices=[(0, 0), (2, 0), (1, 3)])
sage: s.opposite_edge(0, 0)
(1, 1)
sage: tb.clockwise_edge(0,0)
SimilaritySurfaceTangentVector in polygon 1 based at (2, 0) with vector (-1, 3)
edge(polygon_label, edge_index)[source]

Return the vector leaving a vertex of the polygon which under straight-line flow travels counterclockwise around the boundary of the polygon along the edge with the provided index. The length of the vector matches the length of the indexed edge.

EXAMPLES:

sage: from flatsurf.geometry.similarity_surface_generators import SimilaritySurfaceGenerators
sage: s = SimilaritySurfaceGenerators.example()
sage: from flatsurf.geometry.tangent_bundle import SimilaritySurfaceTangentBundle
sage: tb = SimilaritySurfaceTangentBundle(s)
sage: s.polygon(0)
Polygon(vertices=[(0, 0), (2, -2), (2, 0)])
sage: tb.edge(0,0)
SimilaritySurfaceTangentVector in polygon 0 based at (0, 0) with vector (2, -2)
field()
surface()[source]

Return the surface this bundle is over.

vector_space()[source]

Return the vector space over the field of the bundle.

class flatsurf.geometry.tangent_bundle.SimilaritySurfaceTangentVector(tangent_bundle, polygon_label, point, vector)[source]

Tangent vector to a similarity surface.

EXAMPLES:

sage: from flatsurf import translation_surfaces

Examples on edges in direction of edges:

sage: s = translation_surfaces.square_torus()
sage: s.tangent_vector(0, (1/2, 0), (1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (1/2, 0) with vector (1, 0)
sage: s.tangent_vector(0, (1/2, 0), (-1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (1/2, 1) with vector (-1, 0)
sage: s.tangent_vector(0, (1/2, 1), (1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (1/2, 0) with vector (1, 0)
sage: s.tangent_vector(0, (1/2, 1), (-1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (1/2, 1) with vector (-1, 0)

sage: s.tangent_vector(0, (0, 1/2), (0, 1))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 1/2) with vector (0, 1)
sage: s.tangent_vector(0, (0, 1/2), (0, -1))
SimilaritySurfaceTangentVector in polygon 0 based at (0, 1/2) with vector (0, -1)
sage: s.tangent_vector(0, (1, 1/2), (0, 1))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 1/2) with vector (0, 1)
sage: s.tangent_vector(0, (1, 1/2), (0, -1))
SimilaritySurfaceTangentVector in polygon 0 based at (0, 1/2) with vector (0, -1)

Examples on vertices in direction of edges:

sage: s = translation_surfaces.square_torus()
sage: s.tangent_vector(0, (0, 0), (1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (0, 0) with vector (1, 0)
sage: s.tangent_vector(0, (1, 0), (-1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 1) with vector (-1, 0)
sage: s.tangent_vector(0, (0, 1), (1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (0, 0) with vector (1, 0)
sage: s.tangent_vector(0, (1, 1), (-1, 0))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 1) with vector (-1, 0)

sage: s.tangent_vector(0, (0, 0), (0, 1))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 0) with vector (0, 1)
sage: s.tangent_vector(0, (0, 1), (0, -1))
SimilaritySurfaceTangentVector in polygon 0 based at (0, 1) with vector (0, -1)
sage: s.tangent_vector(0, (1, 0), (0, 1))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 0) with vector (0, 1)
sage: s.tangent_vector(0, (1, 1), (0, -1))
SimilaritySurfaceTangentVector in polygon 0 based at (0, 1) with vector (0, -1)
bundle()[source]

Return the tangent bundle containing this vector.

clockwise_to(w, code=False)[source]

Return the new tangent vector obtained by rotating this one in the clockwise direction until the vector is parallel to w, and scaling so that the length matches that of w.

Note that we always do some rotation so that if w is parallel to this vector, then a -360 degree rotation is performed.

The vector w must be nonzero.

On an infinite surface, this is potentially an infinite calculation so we impose a limit (representing the maximal number of polygons that must be rotated through). This is the variable rotate_limit in this package.

If code is True, we compute the sequences of numbers associated to edges crossed as a list. We return a pair consisting of the newly computing tangent vector an this code. This is currently only implemented when based at a singularity.

EXAMPLES:

sage: from flatsurf import translation_surfaces
sage: s = translation_surfaces.regular_octagon()
sage: v = s.tangent_vector(0, (0,0), (1,1))
sage: v.clockwise_to((-1,-1))
SimilaritySurfaceTangentVector in polygon 0 based at (0, a + 1) with vector (-1, -1)
sage: v.clockwise_to((1,1))
SimilaritySurfaceTangentVector in polygon 0 based at (-1/2*a, 1/2*a) with vector (1, 1)
sage: v.clockwise_to((1,1), code=True)
(SimilaritySurfaceTangentVector in polygon 0 based at (-1/2*a, 1/2*a) with vector (1, 1), [0, 5, 2])
counterclockwise_to(w, code=False)[source]

Return the new tangent vector obtained by rotating this one in the counterclockwise direction until the vector is parallel to w, and scaling so that the length matches that of w.

Note that we always do some rotation so that if w is parallel to this vector, then a 360 degree rotation is performed.

The vector w must be nonzero.

On an infinite surface, this is potentially an infinite calculation so we impose a limit (representing the maximal number of polygons that must be rotated through). This is the variable rotate_limit in this package.

If code is True, we compute the sequences of numbers associated to edges crossed as a list. We return a pair consisting of the newly computing tangent vector an this code. This is currently only implemented when based at a singularity.

EXAMPLES:

sage: from flatsurf import translation_surfaces
sage: s=translation_surfaces.regular_octagon()
sage: v=s.tangent_vector(0,(0,0),(1,1))
sage: v.counterclockwise_to((-1,-1))
SimilaritySurfaceTangentVector in polygon 0 based at (1/2*a + 1, 1/2*a + 1) with vector (-1, -1)
sage: v.counterclockwise_to((1,1))
SimilaritySurfaceTangentVector in polygon 0 based at (1, 0) with vector (1, 1)
sage: v.counterclockwise_to((1,1), code=True)
(SimilaritySurfaceTangentVector in polygon 0 based at (1, 0) with vector (1, 1), [7, 2, 5])
differs_by_scaling(another_tangent_vector)[source]

Returns true if the other vector just differs by scaling. This means they should lie in the same polygon, be based at the same point, and point in the same direction.

edge_pointing_along()[source]

Returns the pair of (p,e) where p is the polygon label at the base point, and e is the edge this vector points along or none if it does not point along an edge. Here pointing along means that the vector is based at a vertex and represents the vector joining this edge to the next vertex.

forward_to_polygon_boundary()[source]

Flows forward (in the direction of the tangent vector) until the end of the polygon is reached. Returns the tangent vector based at the endpoint which point backward along the trajectory.

NOTES:

We return the backward trajectory, because continuing forward does not make sense if a
singularity is reached. You can obtain the forward vector by subsequently applying invert().

EXAMPLES:

sage: from flatsurf.geometry.similarity_surface_generators import SimilaritySurfaceGenerators
sage: s = SimilaritySurfaceGenerators.example()
sage: from flatsurf.geometry.tangent_bundle import SimilaritySurfaceTangentBundle
sage: tb = SimilaritySurfaceTangentBundle(s)
sage: s.polygon(0)
Polygon(vertices=[(0, 0), (2, -2), (2, 0)])
sage: s.polygon(1)
Polygon(vertices=[(0, 0), (2, 0), (1, 3)])
sage: from flatsurf.geometry.tangent_bundle import SimilaritySurfaceTangentVector
sage: V = tb.surface().base_ring()**2
sage: v = SimilaritySurfaceTangentVector(tb, 0, V((0,0)), V((3,-1)))
sage: v
SimilaritySurfaceTangentVector in polygon 0 based at (0, 0) with vector (3, -1)
sage: v2 = v.forward_to_polygon_boundary()
sage: v2
SimilaritySurfaceTangentVector in polygon 0 based at (2, -2/3) with vector (-3, 1)
sage: v2.invert()
SimilaritySurfaceTangentVector in polygon 1 based at (2/3, 2) with vector (4, -3)
invert()[source]

Returns the negation of this tangent vector. Raises a ValueError if the vector is based at a singularity.’

is_based_at_singularity()[source]

Return the truth value of the statement ‘the base point for this vector is a singularity.’

is_in_boundary_of_polygon()[source]

Return the truth value of the statement ‘the base point for this vector lies on the boundary of one of the polygons making up the surface.’

plot(**kwargs)[source]

Return a plot of this tangent vector.

EXAMPLES:

sage: import flatsurf
sage: S = flatsurf.translation_surfaces.veech_double_n_gon(5)
sage: v = S.tangent_vector(0, (1/8, 1/4), (1/2, 1/4))
sage: S.plot() + v.plot()
Graphics object consisting of 22 graphics primitives
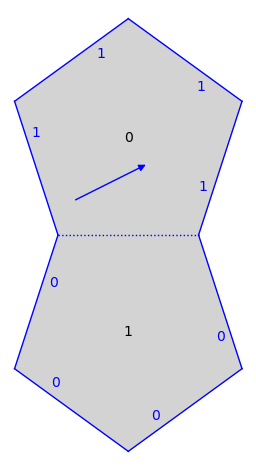
../_images/tangent_bundle_1_0.png

Any keyword arguments are passed on to the underlying plot method from SageMath:

sage: S.plot() + v.plot(color="red")
Graphics object consisting of 22 graphics primitives
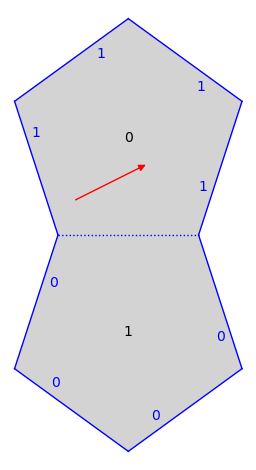
../_images/tangent_bundle_2_0.png
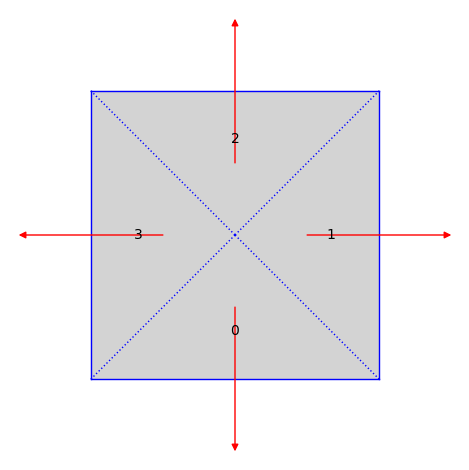
point()[source]

Return the base point of this tangent vector as a vector.

The coordinates of output are given with respect to the polygon it belongs to.

EXAMPLES:

sage: from flatsurf import similarity_surfaces

sage: s = similarity_surfaces.example()
sage: v = s.tangent_vector(0, (1/2,0), (0,1))
sage: v.point()
(1/2, 0)
sage: parent(_)
Vector space of dimension 2 over Rational Field
polygon()[source]
polygon_label()[source]
position()[source]

Return the PolygonPosition representing the location of the basepoint of the vector in the polygon that contains it.

straight_line_trajectory()[source]

Return the straight line trajectory associated to this vector.

EXAMPLES:

sage: from flatsurf import translation_surfaces

sage: s = translation_surfaces.square_torus()
sage: v = s.tangent_vector(0, (0,0), (1,1))
sage: v.straight_line_trajectory()
Straight line trajectory made of 1 segments from (0, 0) in polygon 0 to (1, 1) in polygon 0
sage: l = v.straight_line_trajectory()
sage: l
Straight line trajectory made of 1 segments from (0, 0) in polygon 0 to (1, 1) in polygon 0
sage: l.is_saddle_connection()
True

sage: v = s.tangent_vector(0, (0,0), (1,1+AA(5).sqrt()), ring=AA)
sage: l = v.straight_line_trajectory()
sage: l.flow(20)
sage: l.segment(20)
Segment in polygon 0 starting at (0.9442719099991588?, 0) and ending at (1, 0.1803398874989485?)
surface()[source]

Return the underlying surface.

vector()[source]

Return the coordinates of this vector within the assigned polygon.

EXAMPLES:

sage: from flatsurf import similarity_surfaces

sage: s = similarity_surfaces.example()
sage: v = s.tangent_vector(0, (1/2,0), (0,1))
sage: v.vector()
(0, 1)
sage: parent(_)
Vector space of dimension 2 over Rational Field
vertex()[source]

Return the index of the vertex.