Boshernitzan’s Conjectures

Let \(\Delta\) be a rational triangle and let \(P_0:=P_0(\Delta)\) be the directions for which the flow on the unfolding of \(\Delta\) completely decomposes into cylinders. Let \(E:=E(\Delta)\) be the exceptional directions of \(\Delta\), i.e., the directions for which there exists a generalized diagonal, i.e., a billiard trajectory connecting two vertices.

In Billiards and Rational Periodic Directions in Polygons, Boshernitzan states the following conjecture:

Conjecture 2.2 Assume that a rational triangle \(\Delta=(\alpha, \beta, \chi)\) [is embedded into \(\mathbb{R}^2\) such that one of its sides is horizontal or vertical]. Then:
(a) If \(d\) [with \(d:=\alpha+\beta+\chi\)] is even, we have \(S^1(2d')\subset P_0\) [where \(d':=\mathrm{lcm}(2, d)\) and \(S^1(n):=\{z\in S^1\mid|z^n=1\}\)].
(b) If \(d\) is odd, we have \(S^1(2d')\setminus S^1(d')\subset P_0\).
(c) If \(d\le 12\), and if \(\Delta\ne(2/11,3/11,6/11)\), we have \(S^1(2d')\subset P_0\).
(d) If \(d\le 12\), and if \(\Delta\ne(2/11,3/11,6/11)\) or \((4/11,4/11,3/11)\), we have \(P_0=E\).
(e) If \(\Delta\) is either isosceles, or right triangle, we have \(S^1(2d')\subset P_0\).

In the following, we are trying to verify the statements using sage-flatsurf.

We will find that ❌ (a) does not hold, ❔ (b) might hold, ✔ (c) holds, ❌ (d) does not hold, ❌ (e) does not hold.

(a) Cylinder Periodic Directions of Even Triangles

Let us first state assertion (a) again:

Let \(d\) be even and let \(d=α+β+γ\) be a partition into coprime positive integers. Consider the triangle \(\Delta = (α, β, γ)\), i.e., the triangle with angles \((απ/d, βπ/d, γπ/d)\), embedded into the complex plane such that one of its sides is horizontal. Let \(z\in S^1\) be such that \(z^{2d}=1\). Then the flow in direction \(z\) on the unfolding of \(\Delta\) completely decomposes into cylinders.

To verify this conjecture for a given triangle, we do not need to compute the flow decomposition for each such \(z\) due to symmetries in the unfolding. Indeed, identifying the set \(S^1(2d):=\{z^{2d}=1\}\) with \(\mathbb{Z}/2d\mathbb{Z}\) we see that the assertion holds for a direction \(v\) iff it holds for the subset \(v + \langle 2α, 2β, 2γ\rangle\). Since the angles \(α,β,γ\) are coprime, it suffices to check two directions; for example two directions orthogonal (or equally parallel) to edges of \(\Delta\) that do not meet at the one “even” angle from \(α,β,γ\).

We performed such a search systematically with flatsurvey which is built upon sage-flatsurf. An exhaustive search up to d=153 found 9 counterexamples to the conjecture, namely (7, 7, 16), (7, 8, 15), (13, 20, 23), (15, 30, 47), (11, 45, 50), (23, 29, 58), (19, 38, 55), (11, 22, 103), (30, 41, 67).

Let us verify that the (7, 7, 16) triangle indeed fails the assertion of the conjecture.

First, we construct a triangle with angles (7, 7, 16).

from flatsurf import EuclideanPolygonsWithAngles

Δ = EuclideanPolygonsWithAngles(7, 7, 16).an_element()
Δ

Polygon(vertices=[(0, 0), (1, 0), (1/2, c^7 - 13/2*c^5 + 21/2*c^3 - 3/2*c)])

We unfold this triangle and obtain a translation surface.

from flatsurf import similarity_surfaces

S = similarity_surfaces.billiard(Δ).minimal_cover(cover_type="translation")
S.plot(edge_labels=False, polygon_labels=False)

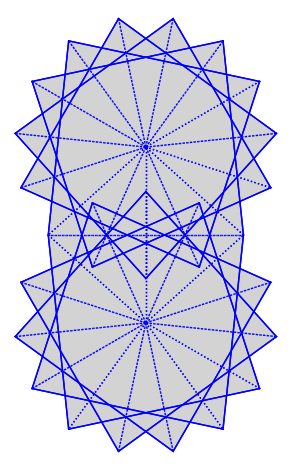
We construct the flow decomposition in direction (0, 1), orthogonal to one of the sides of the triangle.

from flatsurf import GL2ROrbitClosure

D = GL2ROrbitClosure(S).decomposition(vector(Δ.base_ring(), (0, 1)))
D

FlowDecomposition with 6 cylinders, 4 minimal components and 0 undetermined components

We can visualize the complement of the minimal components if ipvue-flatsurf is available. (Note that visualizing the minimal components themselves might not work correctly until #62 has ben resolved.)

from ipyvue_flatsurf import Widget

cylinders = [c for c in D.components() if c.cylinder()]
Widget(cylinders)

(b) Cylinder Periodic Directions of Odd Triangles

Assertion (b) can be phrased as follows:

Let \(d\) be odd and let \(d=α+β+γ\) be a partition into coprime positive integers. Consider the triangle \(\Delta=(α,β,γ)\), i.e., the triangle with angles \((α\pi/d, β\pi/d, γ\pi/d)\), embedded into the complex plane such that one of its sides is horizontal. Let \(z\in S^1\) be such that \(z^{2d}=-1\). Then the flow in direction \(z\) on the unfolding of \(\Delta\) completely decomposes into cylinders.

Again, we do not need to compute the flow decomposition for each such \(z\) since there are a lot of symmetries. Let us identify the \(z\in S^1\) with \(z^{4d}=1\) with \(\mathbb{Z}/4d\mathbb{Z}\). The assertion then holds for a direction \(v\) iff it holds for the subset \(v + \langle 4α, 4β, 4γ\rangle\). Since the \(α,β,γ\) are coprime and the assertion excludes directions with \(z^{2d}=1\), it suffices to check two directions; for example directions orthogonal to two edges of \(\Delta\) that do not meet at an “even” angle.

We performed such a search systematically with flatsurvey which is built upon sage-flatsurf. An exhaustive search up to d=189 found no counterexamples to the conjecture.

(c) Cylinder Periodic Directions of Most Small Triangles

Assertion (c) is a finite variant of (a) and (b), namely it asserts that:

• (a) holds for all \(d\le 12\) and

• (b) holds for all \(d\le 12\) even if we replace \(z^{2d}=-1\) with \(z^{4d}=1\) as long as we exclude the triangle \((2, 3, 6)\).

We can use sage-flatsurf to verify that this assertion does indeed hold. Let us for example verify here that the assertion holds for the (1, 1, 10) triangle.

We start by constructing the unfolding of that triangle:

from flatsurf import EuclideanPolygonsWithAngles, similarity_surfaces

Δ = EuclideanPolygonsWithAngles(1, 1, 10).an_element()
S = similarity_surfaces.billiard(Δ).minimal_cover(cover_type="translation")

We find that this completely decomposes into cylinders in horizontal direction:

from flatsurf import GL2ROrbitClosure

D = GL2ROrbitClosure(S).decomposition(vector(Δ.base_ring(), (0, 1)))
D

FlowDecomposition with 6 cylinders, 0 minimal components and 0 undetermined components

We can visualize these cylinders if ipyvue-flatsurf is available:

from ipyvue_flatsurf import Widget

Widget(D)

The (2, 3, 6) Triangle

As indicated in the conjecture, (2, 3, 6) is exceptional, i.e., there is such a direction for which the flow decomposition does not fully decompose into cylinders.

Computing a Flow Decomposition for the (2, 3, 6) Triangle

Again, we can ask sage-flatsurf to compute the flow decomposition of the unfolding of the (2, 3, 6) triangle. It turns out that in vertical direction (1, 0), it does not fully decompose into cylinders:

from flatsurf import EuclideanPolygonsWithAngles, similarity_surfaces, GL2ROrbitClosure

Δ = EuclideanPolygonsWithAngles(2, 3, 6).an_element()
S = similarity_surfaces.billiard(Δ).minimal_cover(cover_type="translation")
D = GL2ROrbitClosure(S).decomposition(vector(Δ.base_ring(), (1, 0)))
D

FlowDecomposition with 3 cylinders, 2 minimal components and 0 undetermined components

from flatsurf import polygons, similarity_surfaces, EuclideanPolygonsWithAngles
from flatsurf import GL2ROrbitClosure

E = EuclideanPolygonsWithAngles(2, 3, 6)
T = E.random_element()
S = similarity_surfaces.billiard(T)
S = S.minimal_cover(cover_type="translation")
O = GL2ROrbitClosure(S)
D = O.decomposition(vector((1, 0)))
D

FlowDecomposition with 3 cylinders, 2 minimal components and 0 undetermined components

Using ipyvue-flatsurf, we can visualize the minimal components:

from ipyvue_flatsurf import Widget

Widget([component for component in D.components() if component.withoutPeriodicTrajectory()])

Asserting Minimality on the Level of the Interval Exchange Transformation

Internally, the preceding computation is performed on Interval Exchange Transformations describing this translation surface. We are now getting that same result by going through (some of) these underlying steps explicitly with more low-level interfaces.

Currently, the only way to work with such low-level objects is by invoking functions in the C++ libraries libflatsurf and libintervalxt directly. We start by passing from our translation surface to the corresponding surface in libflatsurf. (Note that these operations are not considered part of the stable interface of sage-flatsurf and subject to change.)

F = S.pyflatsurf().codomain().flat_triangulation()

A Unique Large Edge

We start by retriangulating our surface. Namely, we want to obtain a single large edge for the flow direction, i.e., a unique edge that is wider (perpendicular to the flow direction) than all the other edges.

import pyflatsurf

V = pyflatsurf.flatsurf.Vector[type(F).Coordinate]
horizontal = V(int(1), int(0))

F = pyflatsurf.flatsurf.FlatTriangulationCollapsed[type(F).Coordinate](F, horizontal)
pyflatsurf.flatsurf.IntervalExchangeTransformation[type(F)].makeUniqueLargeEdges(
    F, horizontal
)

Unfortunately, we cannot display a plot of such a surface since it is not a real translation surface anymore. Some of the edges (the ones is direction of the flow) have been collapsed, see #62.

large = [e for e in F.edges() if F.vertical().large(e.positive())][0].negative()
large

-12

Flowing from the Large Edge to Construct an Interval Exchange Transformation

We (unfortunately do not) see in the above plot how the half edges on the left get shuffled to be become the half edges on the right if we follow the flow across the large edge.

This defines an Interval Exchange Transformation.

import pyintervalxt, pyeantic

iet = pyflatsurf.flatsurf.IntervalExchangeTransformation[type(F)](
    F, F.vertical().vertical(), large
).forget()
iet

[a: (-6*c^9 + 57*c^7 - 186*c^5 + 240*c^3 - 99*c ~ 0.78634875)] [b: (3*c^9 - 27*c^7 + 84*c^5 - 108*c^3 + 51*c ~ 0.76710082)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [d: (-6*c^9 + 60*c^7 - 213*c^5 + 315*c^3 - 159*c ~ 0.41899073)] [e: (6*c^9 - 60*c^7 + 210*c^5 - 297*c^3 + 135*c ~ 0.50430379)] [f: (3*c^9 - 27*c^7 + 84*c^5 - 108*c^3 + 51*c ~ 0.76710082)] [g: (-3*c^7 + 24*c^5 - 57*c^3 + 36*c ~ 1.2906525)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [i: (-3*c^3 + 12*c ~ 0.48113668)] / [g] [b] [d] [i] [e] [a] [c] [h] [f]

Zorich Induction on the Interval Exchange Transformation

We now attempt to decompose the Interval Exchange Transformation by performing some Zorich induction steps.

Namely, we begin by subtracting a at the top from g at the bottom.

iet.swap()
iet.zorichInduction()
iet.swap()
iet

[b: (3*c^9 - 27*c^7 + 84*c^5 - 108*c^3 + 51*c ~ 0.76710082)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [d: (-6*c^9 + 60*c^7 - 213*c^5 + 315*c^3 - 159*c ~ 0.41899073)] [e: (6*c^9 - 60*c^7 + 210*c^5 - 297*c^3 + 135*c ~ 0.50430379)] [f: (3*c^9 - 27*c^7 + 84*c^5 - 108*c^3 + 51*c ~ 0.76710082)] [a: (-6*c^9 + 57*c^7 - 186*c^5 + 240*c^3 - 99*c ~ 0.78634875)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 297*c^3 + 135*c ~ 0.50430379)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [i: (-3*c^3 + 12*c ~ 0.48113668)] / [g] [b] [d] [i] [e] [a] [c] [h] [f]

Next, we subtract g at the bottom from b at the top.

iet.zorichInduction()
iet

[b: (-3*c^9 + 33*c^7 - 126*c^5 + 189*c^3 - 84*c ~ 0.26279702)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [d: (-6*c^9 + 60*c^7 - 213*c^5 + 315*c^3 - 159*c ~ 0.41899073)] [e: (6*c^9 - 60*c^7 + 210*c^5 - 297*c^3 + 135*c ~ 0.50430379)] [f: (3*c^9 - 27*c^7 + 84*c^5 - 108*c^3 + 51*c ~ 0.76710082)] [a: (-6*c^9 + 57*c^7 - 186*c^5 + 240*c^3 - 99*c ~ 0.78634875)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 297*c^3 + 135*c ~ 0.50430379)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [i: (-3*c^3 + 12*c ~ 0.48113668)] / [g] [b] [d] [i] [e] [a] [c] [h] [f]

Now, we subtract b at the top from g at the bottom.

iet.swap()
iet.zorichInduction()
iet.swap()
iet

[d: (-6*c^9 + 60*c^7 - 213*c^5 + 315*c^3 - 159*c ~ 0.41899073)] [e: (6*c^9 - 60*c^7 + 210*c^5 - 297*c^3 + 135*c ~ 0.50430379)] [f: (3*c^9 - 27*c^7 + 84*c^5 - 108*c^3 + 51*c ~ 0.76710082)] [a: (-6*c^9 + 57*c^7 - 186*c^5 + 240*c^3 - 99*c ~ 0.78634875)] [b: (-3*c^9 + 33*c^7 - 126*c^5 + 189*c^3 - 84*c ~ 0.26279702)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [i: (-3*c^3 + 12*c ~ 0.48113668)] / [g] [b] [d] [i] [e] [a] [c] [h] [f]

We keep going like this for a few more iterations and end up with the starting labels f and e of the same length.

iet.zorichInduction()
iet.swap()
iet.zorichInduction()
iet.swap()
iet.zorichInduction()
iet.swap()
iet.zorichInduction()
iet.swap()
iet.zorichInduction()
iet

[f: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [a: (-6*c^9 + 57*c^7 - 186*c^5 + 240*c^3 - 99*c ~ 0.78634875)] [d: (-15*c^9 + 147*c^7 - 507*c^5 + 714*c^3 - 321*c ~ 0.10985948)] [b: (12*c^9 - 114*c^7 + 381*c^5 - 525*c^3 + 237*c ~ 0.15293754)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [e: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [i: (-3*c^9 + 33*c^7 - 126*c^5 + 189*c^3 - 84*c ~ 0.26279702)] / [e] [a] [c] [h] [i] [b] [g] [d] [f]

Therefore, we can simplify the interval exchange transformation by dropping the label f.

iet.induce(int(0))
iet

[a: (-6*c^9 + 57*c^7 - 186*c^5 + 240*c^3 - 99*c ~ 0.78634875)] [d: (-15*c^9 + 147*c^7 - 507*c^5 + 714*c^3 - 321*c ~ 0.10985948)] [b: (12*c^9 - 114*c^7 + 381*c^5 - 525*c^3 + 237*c ~ 0.15293754)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [e: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [i: (-3*c^9 + 33*c^7 - 126*c^5 + 189*c^3 - 84*c ~ 0.26279702)] / [a] [c] [h] [i] [b] [g] [d] [e]

Now, top and bottom start with the same label a. We found a cylinder.

We continue with the remaining interval exchange transformation.

iet = iet.reduce().value()
iet

[d: (-15*c^9 + 147*c^7 - 507*c^5 + 714*c^3 - 321*c ~ 0.10985948)] [b: (12*c^9 - 114*c^7 + 381*c^5 - 525*c^3 + 237*c ~ 0.15293754)] [c: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] [h: (-3*c^9 + 33*c^7 - 129*c^5 + 210*c^3 - 120*c ~ 0.70495487)] [e: (3*c^9 - 33*c^7 + 126*c^5 - 192*c^3 + 96*c ~ 0.21833966)] [i: (-3*c^9 + 33*c^7 - 126*c^5 + 189*c^3 - 84*c ~ 0.26279702)] / [c] [h] [i] [b] [g] [d] [e]

A few more induction steps, let us drop the e label as we did before.

iet.induce(-int(1))
iet

[d: (-12*c^9 + 126*c^7 - 462*c^5 + 675*c^3 - 303*c ~ 0.021290252)] [h: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] [c: (12*c^9 - 120*c^7 + 423*c^5 - 612*c^3 + 294*c ~ 0.085313060)] [g: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] [b: (-6*c^9 + 66*c^7 - 252*c^5 + 381*c^3 - 180*c ~ 0.044457365)] [i: (-9*c^9 + 81*c^7 - 255*c^5 + 333*c^3 - 141*c ~ 0.065402118)] / [h] [d] [c] [b] [g] [i]

Now, top and bottom start with the same labels d and h. The interval exchange transformation splits.

Let us consider the first part on the labels d and h.

iet.reduce()
iet

[d: (-12*c^9 + 126*c^7 - 462*c^5 + 675*c^3 - 303*c ~ 0.021290252)] [h: (6*c^9 - 60*c^7 + 210*c^5 - 294*c^3 + 123*c ~ 0.023167114)] / [h] [d]

We see that this must be a minimal component. Indeed, consider a point somewhere on the bottom interval, i.e., on either h or d. As this point flows to the top, it either hits d or h there. If it hits d it gets translated by the length of h. If it hits h it gets translated by the length of -d. If there were a cylinder hidden in this somewhere, we would be able to chain such translations together to get a total translation of zero. However, there is no combination of positive integer multiples of h and -d that sums to zero. There cannot be a cylinder.

iet.boshernitzanNoPeriodicTrajectory()

True

We have found a cylinder and a minimal component. Performing the same steps on the other part formed by the labels c, b, g, i yields two more cylinders and another minimal component.

(d) Most Small Triangles are Completely Cylinder Periodic

Assertion (d) can be phrased as

Let \(d\le 12\) with a partition \(d=α+β+γ\) into positive coprime integers with \((α,β,γ)\ne(2,3,6)\) and \((α,β,γ)\ne(3,4,4)\). Consider a triangle \(\Delta=(α,β,γ)\), i.e., the triangle with angles \((α\pi/d, β\pi/d, γ\pi/d)\). Then \(\Delta\) is completely cylinder periodic, i.e., the flow in direction \(v\) on the unfolding of \(\Delta\) decomposes into cylinders for any direction \(v\) given by a saddle connection.

We can use sage-flatsurf to check this assertion for some small triangles. Let us consider the (2, 2, 3) triangle.

from flatsurf import EuclideanPolygonsWithAngles, similarity_surfaces, GL2ROrbitClosure

Δ = EuclideanPolygonsWithAngles(2, 2, 3).an_element()
S = similarity_surfaces.billiard(Δ).minimal_cover(cover_type="translation")

from ipyvue_flatsurf import Widget

Widget(S)

We can compute flow decompositions for some short saddle connections in this surface and look for minimal components.

for connection in S.saddle_connections(4):
    decomposition = GL2ROrbitClosure(S).decomposition(connection.direction())
    if any(
        component.withoutPeriodicTrajectory()
        for component in decomposition.components()
    ):
        print(
            "Found minimal component in",
            decomposition,
            "for direction",
            connection.direction(),
        )
        break

Found minimal component in FlowDecomposition with 0 cylinders, 2 minimal components and 0 undetermined components for direction (1, -9/29*c^5 + 50/29*c^3 - 57/29*c)

We can try to visualize the minimal components. There might be some rendering errors due to #62 however:

from ipyvue_flatsurf import Widget

Widget(decomposition)

(e) Cylinder Periodic Directions of Isosceles and Right Triangles

Assertion (e) can be phrased as

Let \(d=α+β+γ\) be a sum of positive coprime integers with \(γ=α+β\) or \(α=β\). Consider the (right) triangle \(\Delta=(α,β,γ)\) embedded into the complex plane such that one of its sides is horizontal. Let \(z\in S^1\) be such that \(z^{2\mathrm{lcm}(2,d)}=1\). Then the flow in direction \(z\) on the unfolding of \(\Delta\) completely decomposes into cylinders.

The (7,8,15) triangle which is also a counterexample to (a) works here as well.

from flatsurf import EuclideanPolygonsWithAngles, similarity_surfaces, GL2ROrbitClosure

Δ = EuclideanPolygonsWithAngles(7, 8, 15).an_element()
S = similarity_surfaces.billiard(Δ).minimal_cover(cover_type="translation")

from ipyvue_flatsurf import Widget

Widget(S)

from flatsurf import GL2ROrbitClosure

D = GL2ROrbitClosure(S).decomposition(vector(Δ.base_ring(), (1, 0)))
D

FlowDecomposition with 6 cylinders, 2 minimal components and 0 undetermined components