Defining Surfaces

Built in surfaces

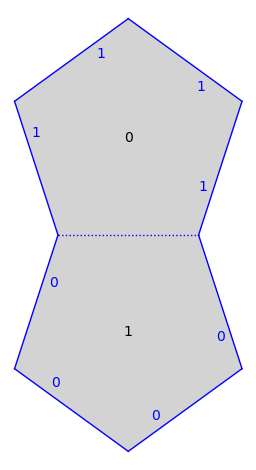
Veech’s double n-gon surfaces:

from flatsurf import translation_surfaces

s = translation_surfaces.veech_double_n_gon(5)
s.plot()

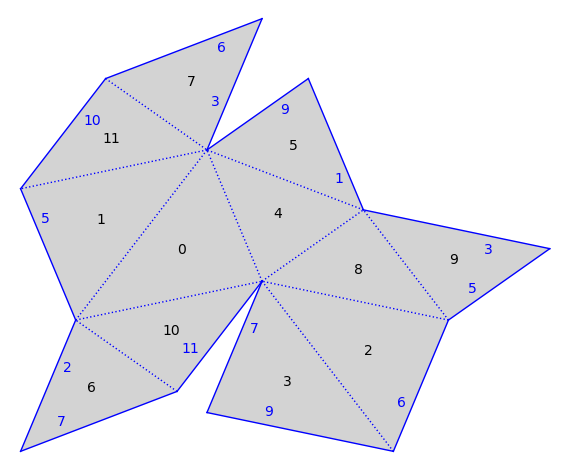
The Arnoux-Yoccoz surface of arbitrary genus is built in:

s = translation_surfaces.arnoux_yoccoz(3)
s.plot()

Chamanara’s infinite translation surface:

s = translation_surfaces.chamanara(1 / 2)

s.plot(polygon_labels=False, edge_labels=False)

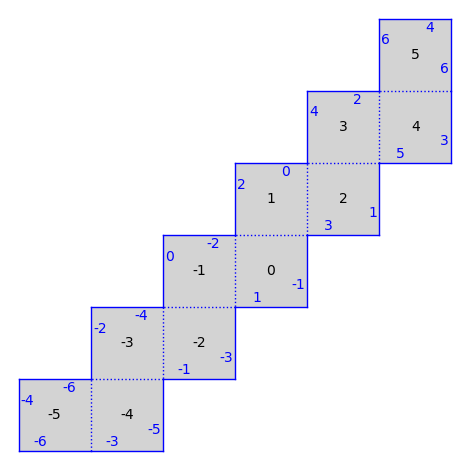
s = translation_surfaces.infinite_staircase()

s.plot()

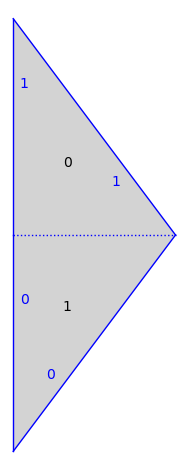
Billiard tables

from flatsurf import similarity_surfaces, Polygon

s = similarity_surfaces.billiard(Polygon(vertices=[(0, 0), (3, 0), (0, 4)]))

s.plot()

Minimal translation surface covers

Continuing the billiard example above, we get an infinite translation surface below:

ss = s.minimal_cover(cover_type="translation")

gs = ss.graphical_surface()

gs.make_all_visible(limit=12)

gs.plot()

Building surfaces from polygons

This defines a regular 12-gon with algebraic real coordinates (AA) with first vector given by (1,0):

from flatsurf import polygons

p0 = polygons.regular_ngon(12, field=AA)
p1 = polygons.regular_ngon(3, field=AA)

p0.plot() + p1.plot()

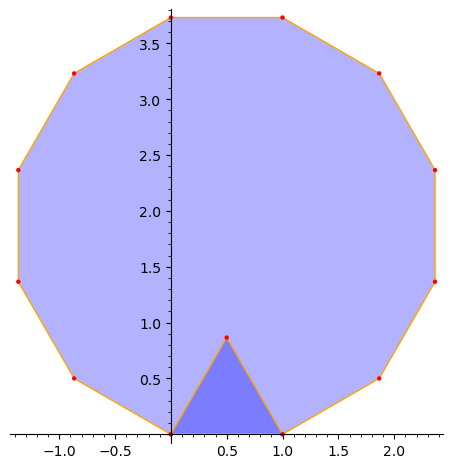
The vertices of n-gons are numbered by \(\{0,...,n-1\}\), with the \(0\)-th vertex at the origin. Edge \(i\) joins vertex \(i\) to vertex \(i+1 \pmod{n}\).

We can act on polygon with \(2 \times 2\) matrices. We define the rotation by \(\frac{\pi}{6}\) below:

R = matrix(AA, [[cos(pi / 6), -sin(pi / 6)], [sin(pi / 6), cos(pi / 6)]])
show(R)

\(\displaystyle \left(\begin{array}{rr} 0.866025403784439? & -\frac{1}{2} \\ \frac{1}{2} & 0.866025403784439? \end{array}\right)\)

R * p1

Polygon(vertices=[(0, 0), (0.866025403784439?, 0.50000000000000000?), (0.?e-18, 1.000000000000000?)])

Define a surface over the field AA of algebraic reals.

from flatsurf import MutableOrientedSimilaritySurface

surface = MutableOrientedSimilaritySurface(AA)

Add two polygons to the surface with labels 0 and 1:

surface.add_polygon(p0, label=0)

0

surface.add_polygon(p1, label=1)

1

Glue the edges of polygon 0 to the parallel edges of polygon 1.

surface.glue((0, 6), (1, 0))
surface.glue((0, 10), (1, 1))
surface.glue((0, 2), (1, 2))

Add three more rotated triangles and glue them appropriately.

for i in range(1, 4):
    surface.add_polygon((R**i) * p1, label=i + 1)
    surface.glue((0, 6 + i), (i + 1, 0))
    surface.glue((0, (10 + i) % 12), (i + 1, 1))
    surface.glue((0, 2 + i), (i + 1, 2))

Now we have a closed surface. In fact this is a translation surface:

surface

Translation Surface built from 4 equilateral triangles and a regular dodecagon

Once we are done building the surface, it is recommended to make the surface immutable. This lets sage-flatsurf figure out of which nature this surface is, e.g., that it is a translation surface. This speeds up many operations on the surface and makes it possible to compute things that are only defined or implemented for some types of surfaces:

surface.set_immutable()
surface

Translation Surface in H_4(6) built from 4 equilateral triangles and a regular dodecagon

If you want to compute things, such as the stratum without making a surface immutable, please refer to the details in the documentation of the flatsurf.geometry.categories module in the module reference.

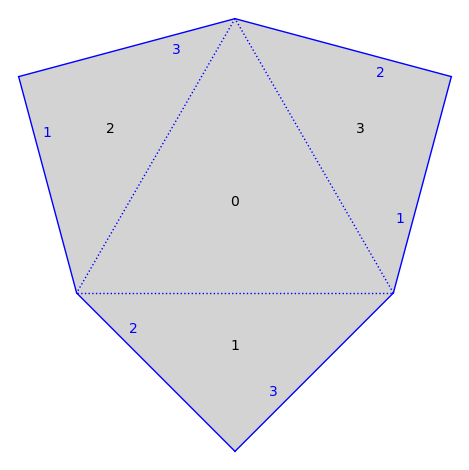
We can plot the surface. Edges are labeled according to the polygon they are glued to.

surface.plot()

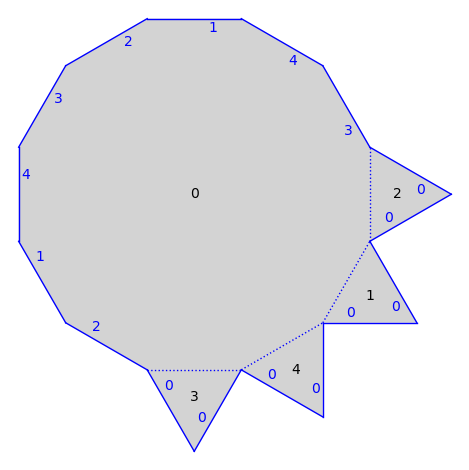
The field containing the vertices:

surface.base_ring()

Algebraic Real Field

Computations in the Algebraic Real Field (AA) are slow. It is better to use a NumberField. The following finds a smaller number field::

vertices = [surface.polygon(p).vertex(v) for (p, v) in surface.edges()]
vertices = [vertex[0] for vertex in vertices] + [vertex[1] for vertex in vertices]
base_ring = Sequence(
    [coordinate.as_number_field_element()[1] for coordinate in vertices]
).universe()
ss = surface.change_ring(base_ring)

ss.base_ring()

Number Field in a with defining polynomial y^2 - 3

Getting a surface from Flipper

Flipper is a program written by Mark Bell which understands mapping classes and can compute the flat structure associated to a pseudo-Anosov mapping class. FlatSurf can import this structure.

This code below requires flipper to be installed. You can do this by running the shell within sage: sage –sh Then within the shell execute: python -m pip install flipper –user –upgrade More information including pitfalls are described in Flipper’s installation instructions.

import flipper

T = flipper.load("SB_4")

h = T.mapping_class("s_0S_1s_2S_3s_1S_2")

h.is_pseudo_anosov()

True

s = translation_surfaces.from_flipper(h)

The surface s is actually a half translation surface

s

Half-Translation Surface in Q_0(-1^4) built from 4 triangles

s.plot()

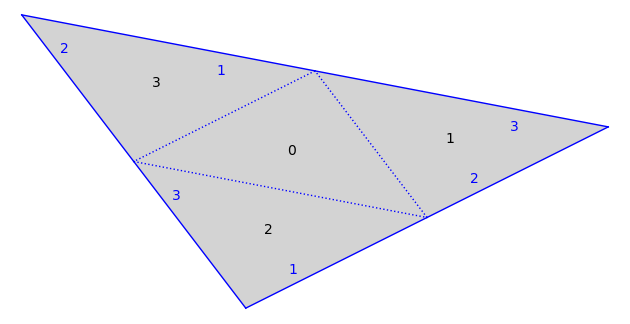
From polyhedra

from flatsurf.geometry.polyhedra import platonic_dodecahedron

polyhedron, s, mapping = platonic_dodecahedron()

The surface \(s\) is a Euclidean cone surface.

s

Genus 0 Rational Cone Surface built from 12 regular pentagons

s.plot()

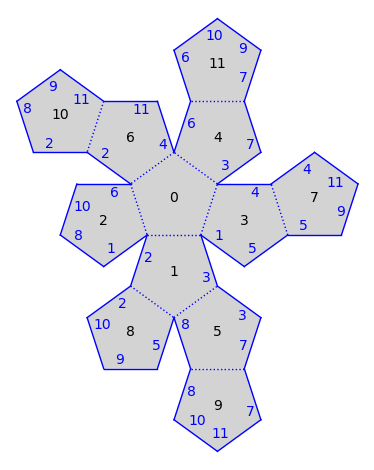
Sage has a built in polyhedron class. You can build a polyhedron as a convex hull of a list of vertices.

polyhedron = Polyhedron([(0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1)])

polyhedron.plot()

The following computes the boundary surface as a Euclidean cone surface. It also provides a map from the surface to the polyhedron.

from flatsurf.geometry.polyhedra import polyhedron_to_cone_surface

s, mapping = polyhedron_to_cone_surface(polyhedron)
s

Genus 0 Rational Cone Surface built from 3 isosceles triangles and an equilateral triangle

s.plot()

Defining an infinite surface from scratch

Finite surfaces can be built by gluing polygons into a MutableOrientedSimilaritySurface. For an infinite surface, we need to subclass OrientedSimilaritySurface and implement a few methods ourselves:

from flatsurf.geometry.surface import OrientedSimilaritySurface
from flatsurf.geometry.categories import TranslationSurfaces


class ParabolaSurface(OrientedSimilaritySurface):
    def __init__(self):
        # For finite surfaces, the category can be determined automotatically
        # but for infinite surfaces, we need to make an explicit choice here.
        super().__init__(
            QQ,
            category=TranslationSurfaces().InfiniteType().WithoutBoundary().Connected(),
        )

    def __repr__(self):
        r"""
        Return a printable representation of this surface.
        """
        return "ParabolaSurface()"

    def roots(self):
        r"""
        Return a label for each connected component of the surface.

        Iterating the polygons of the connected component starts at these labels.
        """
        return (1,)

    def is_mutable(self):
        r"""
        Return whether this surface can be modified by the user.
        """
        return False

    def is_compact(self):
        r"""
        Return whether this surface is a compact space.
        """
        return False

    def __eq__(self, other):
        r"""
        Return whether this surface is indistinguishable from ``other``.
        """
        return isinstance(other, ParabolaSurface)

    def __hash__(self):
        r"""
        Return a hash value for this surface that is compatible with ``__eq``.
        """
        return hash(type(self))

    def graphical_surface(self, **kwds):
        r"""
        Return a plottable representation of this surface.
        """
        graphical_surface = super().graphical_surface(**kwds)
        # Make the first six polygons of the surface visible by default when plotting.
        graphical_surface.make_all_visible(limit=6)
        return graphical_surface

    def polygon(self, label):
        r"""
        Return the polygon making up this surface labeled ``label``.
        """
        if label not in ZZ or label == 0:
            raise ValueError(f"invalid label {label}")

        if label < 0:
            return matrix(QQ, [[-1, 0], [0, -1]]) * self.polygon(-label)

        if label == 1:
            return Polygon(vertices=[(0, 0), (1, 1), (-1, 1)], base_ring=QQ)

        return Polygon(
            vertices=[
                (label - 1, (label - 1) ** 2),
                (label, label**2),
                (-label, label**2),
                (-label + 1, (label - 1) ** 2),
            ],
            base_ring=QQ,
        )

    def opposite_edge(self, label, e):
        if label not in ZZ or label == 0:
            raise ValueError(f"invalid label {label}")
        if label in [-1, 1] and e not in [0, 1, 2]:
            raise ValueError("no such edge")
        if e not in [0, 1, 2, 3]:
            raise ValueError("no such edge")

        if label in [-1, 1] and e == 1:
            return 2 * label, 3

        if e in [0, 2]:
            return -label, e

        if e == 1:
            return label + label.sign(), 3

        return label - label.sign(), 1

s = ParabolaSurface()
s

ParabolaSurface()

s.plot()

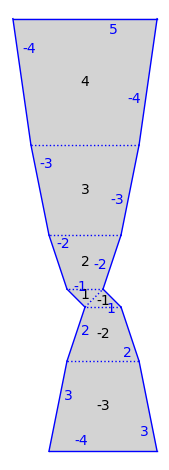
We can run a test suite to ensure that we have implemented everything that is needed to make this a fully functional surface.

TestSuite(s).run(verbose=True)

running ._test_an_element() . . .

 pass

running ._test_cardinality() . . .

 pass

running ._test_category() . . .

 pass

running ._test_components() . . .

 pass

running ._test_construction() . . .

 pass

running ._test_dilation_surface() . . .

 pass

running ._test_elements() . . .

  Running the test suite of self.an_element()

  running ._test_category() . . .

 pass

  running ._test_edges() . . .

 pass

  running ._test_edges_ccw() . . .

 pass

  running ._test_eq() . . .

 pass

  running ._test_new() . . .

 pass

  running ._test_not_implemented_methods() . . .

 pass

  running ._test_pickling() . . .

 pass

 pass

running ._test_elements_eq_reflexive() . . .

 pass

running ._test_elements_eq_symmetric() . . .

 pass

running ._test_elements_eq_transitive() . . .

 pass

running ._test_elements_neq() . . .

 pass

running ._test_eq() . . .

 pass

running ._test_gluings() . . .

 pass

running ._test_gluings_without_boundary() . . .

 pass

running ._test_half_translation_surface() . . .

 pass

running ._test_labels_polygons() . . .

 pass

running ._test_new() . . .

 pass

running ._test_not_implemented_methods() . . .

 pass

running ._test_pickling() . . .

 pass

running ._test_polygons() . . .

 pass

running ._test_positive_dilation_surface() . . .

 pass

running ._test_rational_surface() . . .

 pass

running ._test_refined_category() . . .

 pass

running ._test_some_elements() . . .

 pass

running ._test_translation_surface() . . .

 pass