Straight-Line Flow

Acting on surfaces by matrices.

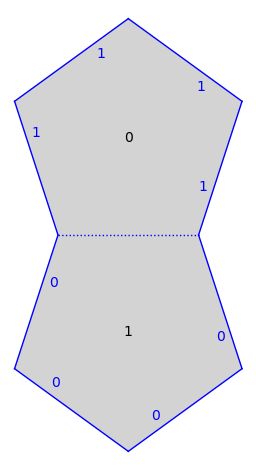
from flatsurf import translation_surfaces

s = translation_surfaces.veech_double_n_gon(5)

s.plot()
../_images/f20207a9fcc190439af6713a23bb04f44336d5b60d4853a4aa33c0672b80fa2d.png

Defines the tangent_bundle on the surface defined over the base_ring of s.

TB = s.tangent_bundle()

baricenter = sum(s.polygon(0).vertices()) / 5

Define the tangent vector based at the baricenter of polygon 0 aimed downward.

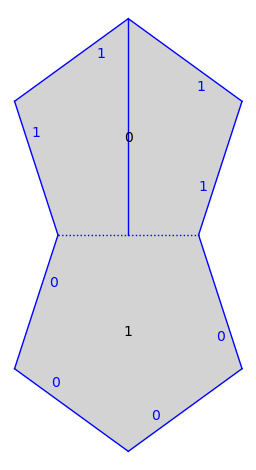
v = TB(0, baricenter, (0, -1))

Convert to a straight-line trajectory. Trajectories are unions of segments in polygons.

traj = v.straight_line_trajectory()

s.plot() + traj.plot()
../_images/7a8800e2fca54300cd6e059a421c71d09c48afda0bc1c952c5cde58b1ac22ad3.png

Flow into the next \(100\) polygons or until the trajectory hits a vertex.

traj.flow(100)

s.plot() + traj.plot()
../_images/003f81d549b8d87e5b497773bfd15f9299d6cae735bebf32d77043d92b8386e1.png

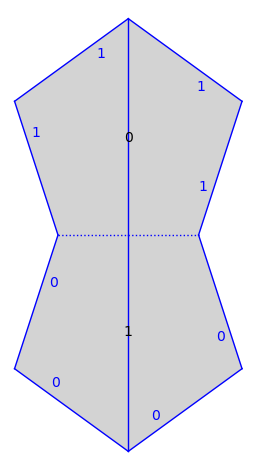
We can tell its type.

traj.is_saddle_connection()

True

You can also test if a straight-line trajectory is closed or a forward/backward separatrix.

Lets do it again but in the slope one direction.

v = TB(0, baricenter, (1, 1))

traj = v.straight_line_trajectory()

traj.flow(100)

s.plot() + traj.plot()
../_images/7bc089384371cd9250ec3fc4aae540caec31f9f414063ad3fcf7c1f15177d933.png

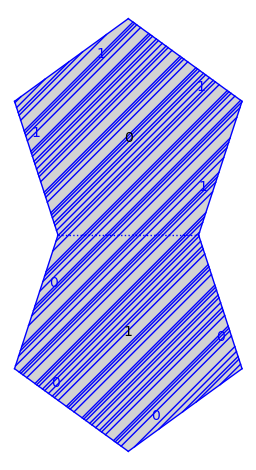
We remark that it follows from work of Veech that the slope one direction is ergodic for the straight-line flow.