Siegel-Veech Constants

We count the number of cylinders of circumference at most \(L\) in a surface as a step in a potential computation of Siegel-Veech constants that David Aulicino was interested in.

Note that parts of this code use the C++ library libflatsurf. Please consult our installation instructions if this library is not available on your system yet.

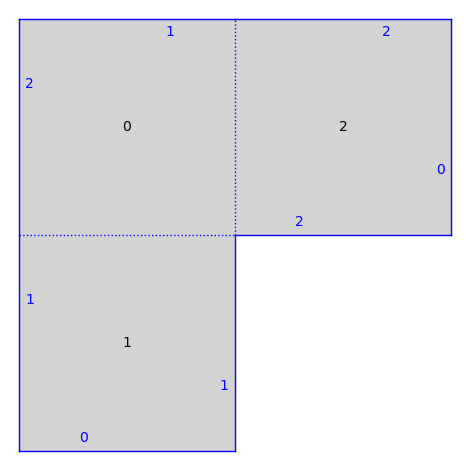
We start by creating a surface with sage-flatsurf.

from flatsurf import translation_surfaces

S = translation_surfaces.mcmullen_L(1, 1, 1, 1)

S.plot()

Decomposition of a surface into cylinders is implemented in pyflatsurf. We triangulate our surface and make sure that its vertices are singularities.

S = S.pyflatsurf().codomain().flat_triangulation()
S = S.eliminateMarkedPoints().surface()

We will iterate over all directions coming from saddle connections of length at most L (ignoring connections that have the same slope).

L = int(16)

directions = S.connections().bound(L).slopes()

For each direction we want to compute a decomposition into cylinders and minimal components. Note that sometimes our algorithm cannot decide whether a component is minimal. However, this is not an issue here: we can stop the decomposition process when a component has become so stretched out that it has no hope of producing a cylinder of circumference \(≤L\) anymore.

Here we define the target of the decomposition, i.e., a predicate that determines when a decomposition of a component can be stopped:

def target(component):
    if component.cylinder():
        # This component is a cylinder. No further decomposition needed.
        return True
    if component.withoutPeriodicTrajectory():
        # This component is minimal. Further decomposition will not produce any cylinders.
        return True

    height = component.height()

    # This height bounds the size of any cylinder. However, it is stretched by the length of the vector
    # defining the vertical direction. (That vector is not normalized because that is hard to do in
    # general rings…)
    from pyflatsurf import flatsurf

    denom = flatsurf.Bound.upper(component.vertical().vertical()).squared()
    return (height * height) / denom > L

Now we perform the actual decomposition and collect the cylinders of circumference \(≤L\):

circumferences = []

for direction in directions:
    from pyflatsurf import flatsurf

    decomposition = flatsurf.makeFlowDecomposition(S, direction.vector())
    decomposition.decompose(target)
    for component in decomposition.components():
        if component.cylinder():
            circumference = component.circumferenceHolonomy()
            if circumference > L:
                continue
            circumferences.append(circumference)

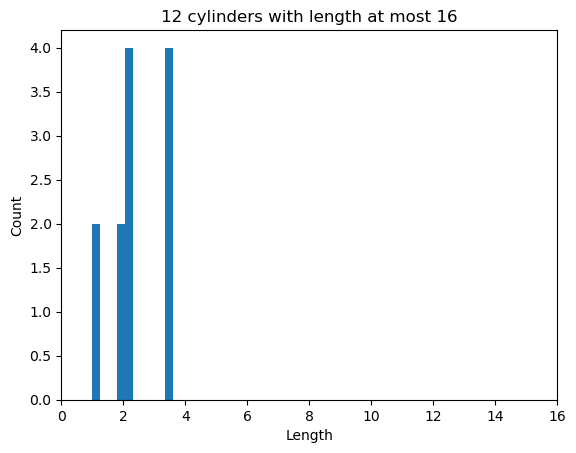
We plot a histogram of all the cylinders we found, ordered by length. It would be easy to plot this differently, weighted by the area, …

lengths = [sqrt(float(v.x()) ** 2 + float(v.y()) ** 2) for v in circumferences]

import matplotlib.pyplot as plot

_ = plot.hist(lengths)
_ = plot.xlim(0, L)
_ = plot.title(f"{len(circumferences)} cylinders with length at most {L}")
_ = plot.xlabel("Length")
_ = plot.ylabel("Count")